MTH/221 Week 1

Everything listed for this week is included in purchase!!

Individual: Week 1 Connect Exercises (and Answers)!

SET #1 - 35 Questions

1.  A particular brand of shirt comes in 12 colors, has a male version and a female version,

     and comes in three sizes for each sex. How many different types of this shirt are made?
2.  (a) Which rule must be used to find the number of strings of four decimal digits that do

     not contain the same digit twice? (b) How many strings of four decimal digits do not

     contain the same digit twice?

     Explanation to Question #2: The product rule must be used since there are 10

     ways to   choose the first digit, 9 ways to choose the second, and so on. If there are n₁

      ways to do the first task and for each of these ways of doing the first task, there are n₂

      ways to do the second task, then there are n₁n₂ ways to do the procedure.

     Therefore you would calculate the answer as: 10 · 9 · 8 · 7 = 5040 ways.

3.  b) Which rule must be used to find the number of strings of four decimal digits that end

     with an even digit? How many strings of four decimal digits end with an even digit?

Explanation to Question #3: The product rule is used in this case, since there are

MTH/221 Week 2

Everything listed for this week is included in purchase!!

** NOTE:  Connect Exercise questions may not be identical to what you have since they are change frequently. However, they are the same type of question, just different numbers involved.  To assist, All Connect Exercise Questions include detailed explanations on how to arrive at the Correct answer (as shown above for #2 and #3 questions).

Individual: Week 2 Connect Exercises

SET #1 - 93 Questions

1. Which of the following is true for the statement “do not pass go”?
2. “What time is it?” is a proposition (yes or no)
3. Which of the following statements are true about the sentence “There are no black flies in Maine”.

SET #2 - 12 Questions

1.  Which of these are propositions? What is the truth value of those that are propositions?
     a) Answer this question.
     b) What time is it?
     c) Miami is the capital of Florida.
     d) 6+x=9
     e) The moon is made of green cheese.
     f) 2n≥130

2.  Let p, q, and r be the propositions
       p:  You have the flu.
       q:  You miss the final examination.
        r:  You pass the course.
    Express each of these propositions as an English sentence.
      a) ¬q→¬p
      b) ¬q↔p
      c) p∨q∨r       
      d) (p→¬r)∨(q→¬r)
      e) (p∧q)∨(¬q∧r)        
3.  State the converse, contrapositive, and inverse of each of these conditional statements.

MTH/221 WEEK 2 Discussion Questions

Supporting Activity

There is an old joke, commonly attributed to Groucho Marx, which goes something like this: "I don't want to belong to any club that will accept people like me as a member." Does this statement fall under the purview of Russell's paradox, or is there an easy semantic way out? Look up the term fuzzy set theory in a search engine of your choice or the University Library, and see if this theory can offer any insights into this statement.

Supporting Activity

How do we distinguish relations from functions?

Supporting Activity

What sort of relation is friendship, using the human or sociological meaning of the word? Is it necessarily reflexive, symmetric, antisymmetric, or transitive? Explain why it is or is not any of these. What other types of interpersonal relationships share one or more of these properties? Explain.

Supporting Activity

Write the dual of the following Boolean equation: a+a'b = a+b?

Supporting Activity

Reduce the following Boolean product to zero OR a fundamental product: xyx'z.

MTH/221 Week 3

Everything listed for this week is included in purchase!!

** NOTE:  Connect Exercise questions may not be identical to what you have since they are change frequently. However, they are the same type of question, just different numbers involved.  To assist, All Connect Exercise Questions include detailed explanations on how to arrive at the Correct answer.

Individual: Week 3 Connect Exercises

SET #1 - 83 Questions

1. Identify the steps that are used to find the maximum element from the following finite

     sequence 1, 8, 12, 9, 11, 2, 14, 5, 10, 4.

2. Rearrange the following algorithm in the correct order to find the sum of all the

     integers in a list.

3. Rearrange the following algorithm that takes as input a list of n integers and products

    as output the largest difference obtained by subtracting an integer in the list from the

    one following it.

SET #2 - 28 Questions

1. List all the steps used by Algorithm 1 to find the maximum of the list 3, 9, 14, 7, 11, 4, 18,

     3, 11, 2.

2. Determine which characteristics of an algorithm described in the text (after Algorithm

     1) the following procedures have and which they lack. Select characteristics that the

      procedures have and leave characteristics unselected that the procedures lack.

3. Which of the following algorithms can be used to find the sum of all integers in a list?

MTH/221 WEEK 3 Class Discussion Questions

Supporting Activity

Supporting Activity

Given this recursive algorithm for computing a factorial...

procedure factorial(n: nonnegative integer)

if n = 0 then return 1

else return n *factorial(n − 1)

{output is n!} Show all the steps used to find 5!

Supporting Activity

Describe an induction process. How does induction process differ from a process of simple repetition?

Supporting Activity

List all the steps used to search for 9 in the sequence 1,3, 4, 5, 6, 8, 9, 11 using a binary search.

MTH/221 Week 4

Everything listed for this week is included in purchase!!

** NOTE:  Connect Exercise questions may not be identical to what you have since they are change frequently. However, they are the same type of question, just different numbers involved.  To assist, All Connect Exercise Questions include detailed explanations on how to arrive at the Correct answer.

Individual: Week 4 Connect Exercises

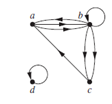
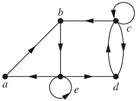
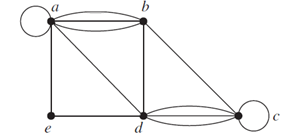
SET #1 - 32 Questions

1. Identify the type of graph.

2. What is the number of vertices of the given graph?

3. Click and drag the vertices (in the right column) to their number of in-degrees (in the

     left column).

SET #2 - 14 Questions

1. Determine whether the graph shown has directed or undirected edges, whether it has

     multiple edges, and whether it has one or more loops. Use your answers to determine

     the type of graph in Table 1.

2. The intersection graph of a collection of sets A1, A2, . . . , An is the graph that has a

     vertex for each of these sets and has an edge connecting the vertices representing

     two sets if these sets have a nonempty intersection. Select the intersection graph of

     these collections of sets.

3. Find the number of vertices, the number of edges, and the degree of each vertex in

     the given undirected graph. Identify all isolated and pendant vertices.

MTH/221 WEEK 4 Class Discussion Questions

Supporting Activity: Hamiltonian and Euler Graphs

Note a Hamiltonian circuit visits each vertex only once but may repeat edges. A Eulerian graph traverses every edge once, but may repeat vertice.

Looking at the figure below tell me if they are Hamiltonian and/or Eulerian.

*-------*--------*
|      /  |   \      |
|   /     |      \   |
|/        |        \ |
*-------*--------*

Supporting Activity: Path Analysis Class
Here is a Question for you:
For the diagram below find all the "simple paths" from A to F.

A------------B------------C
 |               |              / |
 |               |         /      |
 |               |    /           |
D------------E------------F   

Supporting Activity: Random Graphs

Random graphs are a fascinating subject of applied and theoretical research. These can be generated with a fixed vertex set V and edges added to the edge set E based on some probability model, such as a coin flip. Speculate on how many connected components a random graph might have if the likelihood of an edge (v1,v2) being in the set E is 50%. Do you think the number of components would depend on the size of the vertex set V? Explain why or why not.

Supporting Activity: Trees and Language Processing

Trees occur in various venues in computer science: decision trees in algorithms, search trees, and so on. In linguistics, one encounters trees as well, typically as parse trees, which are essentially sentence diagrams, such as those you might have had to do in primary school, breaking a natural-language sentence into its components--clauses, subclauses, nouns, verbs, adverbs, adjectives, prepositions, and so on. What might be the significance of the depth and breadth of a parse tree relative to the sentence it represents? If you need to, look up parse tree and natural language processing on the Internet to see some examples.

MTH/221 - Week 5

Everything listed for this week is included in purchase!!

** NOTE:  Connect Exercise questions may not be identical to what you have since they change frequently. However, they are the same type of question, just different numbers involved.  To assist, All Connect Exercise Questions include detailed explanations on how to arrive at the Correct answer (as shown above for #2 and #3 questions).

Case Study Application Paper
Write a 750- to 1,250-word paper in which you complete one of the following options:

Option 1: Food Webs Case Study
Explainthe theory in your own words based on the case study and suggested readings.
Includethe following in your explanation:
      • Competition
      • Food Webs
      • Boxicity
      • Trophic Status
Givean example of how this could be applied in other real-world applications.
Formatyour paper according to APA guidelines. All work must be properly cited and referenced.

Option 2: Coding Theory Case Study
Explain the theory in your own words based on the case study and suggested readings.
Include the following in your explanation:
      • Error Detecting Codes
      • Error Correcting Codes
      • Hamming Distance
      • Perfect Codes
      • Generator Matrices
      • Parity Check Matrices
      • Hamming Codes
Givean example of how this could be applied in other real-world applications.
Formatyour paper according to APA guidelines. All work must be properly cited and referenced.

FINAL EXAM (2 Sets Included)

40 Questions

1. A particular brand of shirt comes in 8 colors, has a male version and a female version, and comes in 5 sizes for each sex. How many different types of this shirt are made?

2. A club has 22 members.  

a) How many ways are there to choose four members of the club to serve on an executive committee? 
b) How many ways are there to choose a president, vice president, secretary, and treasurer of the club, where no person can hold more than one office? 

After performing some research or based on your reading in the course, share with the class the most practical use of discrete mathematics (in your opinion). Please cite your source.